I put this on my website a long time ago, maybe around 1998, as an HTML page. This is it moved to my blog.

Contents

• Introduction
• Bayesian Probability
• Bayesian Belief Networks

Introduction

Expert systems often calculate the probabilities of inter-dependent events by giving each parent event a weighting. Bayesian Belief Networks provide a mathematically correct and therefore more accurate method of measuring the effects of events on each other. The mathematics involved also allow us to calculate in both directions. So we can, for instance find out which event was the most likely cause of another.

Bayesian Probability

Bayes’ Theorem

You are probably familiar with the following Product Rule of probability for independent events:

p(AB) = p(A) * p(B), where p(AB) means the probability of A and B happening.

This is actually a special case of the following Product Rule for dependent events, where p(A | B) means the probability of A given that B has already occurred:

p(AB) = p(A) * p(B | A)
p(AB) = p(B) * p(A | B)

So because: p(A) p(B | A) = p(B) p(A | B)
We have: p(A | B) = ( p(A) * p(B | A) ) / p(B) which is the simpler version of Bayes’ Theorem.

This equation gives us the probability of A happening given that B has happened, calculated in terms of other probabilities which me may know.

Note that: p(B) = p(B | A) * p(A) + p(B | ~A) * P(~A)

Chaining Bayes’ Theorem

We may wish to calculate p(AB) given that a third event, I, has happened. This is written p(AB | I). We can use the Product Rule: P(A,B) = p(A|B) p(B)

p(AB | I) = p(A | I) * p(B | AI)
p(AB | I) = p(B | I) * p(A | BI)

so we have: p(A | BI) = ( p(A | I) * p(B | AI) ) / p(B | I) which is another version of Bayes’ Theorem.

This gives us the probability of A happening given that B and I have happened.

This is often quoted as p(H | EI) = ( p(H | I) * p(E | HI) ) / p(E | I), where p(H | EI) is the probablity of Hypothesis H given Evidence E in Context I.

By using the product rule we can chain several probabilities together. For instance, to find the probability of H given that E₁, E₂ and I have happened:

p(H | E₁E₂I) = ( p(H | I) * p(E₁E₂ | HI) ) / p(E₁E₂| I)

and to find the probability of H given that E₁, E₂, E₃ and I have happened:

p(H | E₁E₂E₃I) = ( p(H | I) * p(E₁E₂E₃ | HI) ) / p(E₁E₂E₃ | I)

Note that p(E₁E₂E₃ | I) = p(E₁ | E₂E₃I) * p(E₂E₃ | I) = p(E₁ | E₂E₃I) * p(E₂ | E₃I) P(E₃ | I), which can be used to calculate two of the values in the above equation.

An example of Bayes’ Theorem

p(H | EI) = ( p(H | I) * p(E | HI) ) / p(E | I)
p(H | EI) = ( p(H | I) * p(E | HI) ) / ( p(E | HI) * p(H | I) + p(E | ~HI) * p(~H | I) )
H is the Hypothesis ‘Guilty’,
E is an item of evidence,
I is the context.

p(H | EI) is the probability of the Hypothesis ‘Guilty’ being true, given the evidence in this context.
p(H | I) is the Prior Probability – the subjective probability of the Hypothesis regardless of the evidence.
p(E | HI) is the probability of the evidence being true given that the Hypothesis is true.
p(~H | I) = 1 – p(H | I).
p(E | ~HI) is the probability of the evidence given that the hypothesis is not true – this measures the chances of the evidence being caused by something other than the defendant’s guilt. If this is high then naturally the hypothesis will be unlikely.

Assuming Conditional Independence

If, given that I is true, E₁ being true will not affect the probability of E₂ being true, then a simpler version of the chained bayesian theorem is possible:

p(H | E₁E₂I) = ( p(H | I) * p(E₁ | HI) ) * p(E₂ | HI) ) / ( p(E₁ | I) * p(E₂ | I) )

This version makes it very easy to introduce new evidence into the situation. However, Conditional Independence is only true in some special situations.

Prior Probabilities

One characteristic of Bayes’ Theorem is p(H | I), which is the probability of the hypothesis in context I regardless of the evidence. This is referred to as the Prior Probability. It is generally very subjective and is therefore frowned upon. This is not a problem as long the prior probability plays a small role in the result. When the result is overly dependent on the prior probability more evidence should be considered.

Bayesian Belief Networks

A Bayesian Belief Network (BBN) defines various events, the dependencies between them, and the conditional probabilities involved in those dependencies. A BBN can use this information to calculate the probabilities of various possible causes being the actual cause of an event.

Setting up a BBN

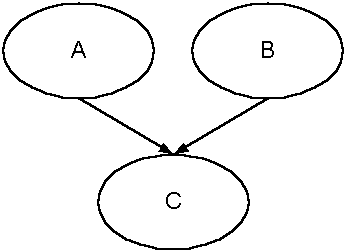
For instance, if event C can be affected by events A and B:

We may know the following probabilities:

A:

True	False
p(A) = 0.1	p(~A) = 0.9

B:

True	False
p(B) = 0.4	p(~B) = 0.6

C: Note that when depencies converge, there may be several conditional probabilites to fill-in, though some can be calculated from others because the probabilities for each state should sum to 1.

A	True		False
B	True	False	True	False
True	p(C | AB) = 0.8	p(C | A~B) = 0.6	p(C | ~AB) = 0.5	p(C | ~A~B) = 0.5
False	p(~C | AB) = 0.2	p(~C | A~B) = 0.4	p(~C | ~AB) = 0.5	p(~C | ~A~B) = 0.5

Calculating Initialised probabilities

Using the known probabilities we may calculate the ‘initialised‘ probability of C, by summing the various combinations in which C is true, and breaking those probabilities down into known probabilities:

p(C) =	p(CAB) + p(C~AB) + p(CA~B) + p(C~A~B)
=	p(C | AB) * p(AB) + p(C | ~AB) * p(~AB) + p(C | A~B) * p(A~B) + p(C | ~A~B) * p(~A~B)
=	p(C | AB) * p(A) * p(B) + p(C | ~AB) * p(~A) * p(B) + p(C | A~B) * p(A) * p(~B) + p(C | ~A~B) * p(~A) * p(~B)
=	0.518

So as a result of the conditional probabilities, C has a 0.518 chance of being true in the absence of any other evidence.

Calculating Revised probabilities

If we know that C is true, we can calculate the ‘revised’ probabilities of A or B being true (and therefore the chances that they caused C to be true), by using Bayes Theorem with the initialised probability:

p(B | C) =	( p( C | B) * p(B) ) / p(C)
=	( ( p(C | AB) * p(A) + p(C | ~AB) * p(~A) ) * p(B) ) / p(C)
=	( (0.8 * 0.1 + 0.5 * 0.9) * 0.4 ) / 0.518
=	0.409

p(A | C) =	( p( C | A) * p(A) ) / p(C)
=	( ( p(C | AB) * p(B) + p(C | A~B) * p(~B) ) * p(A) ) / p(C)
=	( (0.8 * 0.4 + 0.6 * 0.6) * 0.1 ) / 0.518
=	0.131

So we could say that given C is true, B is more likely to be the cause than A.

I put this on my website a long time ago, maybe around 1996, as an HTML page. This is it moved to my blog.

The structure of this explanation is lifted from ‘An Introduction to Symbolic Logic’ by Susanne K. Langer, without her permission.

1.

Content:

The things or material in a system.

Form:

The way in which the contents are related in a system.

Abstraction:

Separating Form from Content, sometimes by discovering analogies.

Interpretation:

Finding possible Content for Forms.

2.

Degree:

Number of Elements used by a Relation. e.g. Dyadic: ‘is north of’, Triadic: ‘is
between’.

Proposition:

Asserts that the Elements are related by the Relation. e.g. ‘Edinburgh’ nt ‘Swindon’.

Symbols:

=int means ‘equals by interpretation’. e.g ‘nt2’ =int ‘is north of’.~ means ‘is not
true’. e.g. ~’Swindon nt Edinburgh’.

3.

Context:

Consists of elements and relations.

e.g. K(‘Brighton’, ‘Swindon’, ‘Edinburgh’) nt₂ =int ‘cities’2 =int ‘is north of’

Universe Of Discourse:

All Elements in the context. e.g. K(a,b,c,…) K=int ‘cities’

Constituent Relations:

The relations used in the context. e.g. nt₂ =int ‘is north of’

Elementary Propositions:

The statements that may be made by relating Elements.

e.g. ‘Edinburgh’ nt ‘Swindon’.

Truth Value:

Whether the Elementary Proposition is true or false. e.g. ‘Swindon’ nt ‘Edinburgh’ is false.

Symbols:

⋅ means Conjunction (‘and’)
∨ means Disjunction (‘or’)
⊃ means Implication (‘implies that’)

Logical Relations:

When the truth of one Elementary Proposition is dependent upon the truth of others they
are Logically Related.

e.g. (‘Edinburgh’ nt ‘Swindon’) ⋅ (‘Swindon’ nt ‘Brighton’) ⊃ (‘Edinburgh’ nt ‘Brighton’)

System of Elements:

Context with Elementary Propositions connected by Logical Relations

4.

Variables:

As in algebra. e.g. x means ‘Edinburgh’ or ‘Swindon’ or ‘Brighton’ etc.

Allows us to summarise Logical Relations of the same form.

e.g. (a nt b) ⋅ (b nt c) ⊃ (a nt c)

Quantifiers:

The Logical Relation may hold for All or Some of the variables.

Universal Quantifier:
(a) means ‘for all a’. e.g. (a) : (a nt b) ⊃ ~(b nt a)

Particular Quantifier:

(∃a) means ‘for at least one a’. e.g. (∃a): (a nt ‘Swindon’)

Propositional Form:

Elementary Proposition or Logical Relation using Variables, whose Truth Value would depend upon the actual Elements substituted. e.g ‘a nt b’.

General Proposition:

Propositional Form with Quantifiers.

5.

Class:

∈ means ‘is a member of’. e.g. ‘Murray’ ∈ B, where B =int ‘Class of Humans’.

General Propositions (see above) concern Classes of Elements.

Defining Form:

Defines the Class in terms of Propositional Forms. The Class contains all elements for which the Propositional Form is True.

Intension:

Meaning of a concept. e.g. the class ‘town’.

Extension:

The elements to which the concept applies. e.g. the class of ‘towns’.

N.B. Classes with unrelated Intensions may share some Elements in Extension.

e.g. ‘Towns north of Swindon’ and ‘Towns with Universities’.

Inclusion:

(x): (x ∈ A) ⊃ (x ∈ B) means Class A is included in Class B, by stating that any Element in A is therefore in B.

Unit Class (I):

Has one member, meaning that if two Elements are both in A then they must both be the
same Element.

(∃x) (y): (x ∈ A) ⋅ [ (y ∈ A) ⊃ (x=y) ]

The Null Class (o):

Has no Elements. There is a single Null Class, because two null classes could not be distinguished.

The Universe Class:

Contains all Elements. There is a single Universe Class.

Mutual Inclusion:

Classes have same Elements so each Class is included in the other.

(x): [ (x ∈ A) ⊃ (x Î B) ] ⋅ [ (x ∈ B) ⊃ (x ∈ A) ]

Class symbols:

< means Inclusion. e.g. A < B means (x): (x ∈ A) ⊃ (x ∈ B)
X means Conjunction (and). e.g. A X B means the Elements which are in A and in B. X is often omitted e.g. AB
+ means Disjunction (or). e.g. A + B means the Elements which are in A or in B.
– means Complement. e.g. -A means the Elements not in A.
= means Mutual Inclusion e.g. A = B means (A < B) . (B < A)

N.B. A<A, A<I, 0<A

Mutual Exclusion:

Classes have no Elements in common.

A X B = o

Dichotomy:

The fact that I = A + -A.

Exclusion:

A < -B means A is excluded from B.

7.

Predicate:

e.g. A, -A, A X B, A + B

Predicative Propositions:

Propositions about Predicates

System of Classes:

K(a,b,c…) <, similar to System of Elements but with Classes instead of Elements and < as the constituent relation.

Dots instead of brackets:

e.g. :. a : b . cd : e instead of ( a . ( b . ( c . d) ) . e)

You’ll get the hang of it.

8.

Calculus of Classes:

Describes the System of Classes for all Classes, just as the Calculus of Numbers
describes the System of Numbers for all Numbers.

Shows how to deduce some Propositions from others.

Postulates.

Basic Propositions of the system. e.g. (a, b) . a + b = b + a.

There are ten Postulates of the Calculus of Classes, analogous to the uses of Venn Diagrams.

Axioms:

Self-evident Postulates that are assumed because they can not be deduced.

9.

Boolean Algebra of Classes

Generalised Calculus of Classes, just as Algebra of Numbers is generalised Calculus of
Numbers.

Laws of Duality

Conjunction can be defined in terms of Disjunction and vice-verse.

Primitive Propositions

The propositions used to prove theorems in Boolean Algebra. They may use either
Conjunction or Disjunction. They show the following:

Operational Assumptions:

Existence of complements, sums, products.

Existential Assumptions:

Existence of Universe Class, Null Class, more than one Class.

Laws of Combination:

Tautology e.g. ‘a + a = a’

Commutation e.g. ‘a + b = b + a’

Association e.g. ‘(a + b) + c = a + (b + c)’

Distribution e.g. ‘a + (b X c) = (a + b) X (a + c)’

Absorption e.g. ‘a + ab = a’

Laws of the Unique Elements:

Universe Class e.g. ‘a + 1 = 1’

Null Class e.g. ‘a + 0 = 0’

Laws of Negation:

Complementation e.g. ‘a + -a = 1’

Contraposition ‘a = -b . ⊃ . b = -a’

Double Negation e.g. ‘a = -(-a)’

Expansion e.g. ‘ab + a-b = a’

Duality e.g. ‘-(a + b) = -a X -b’

10.

System in Abstracto.

K R, where K is the universe of something and R is some way of relating these things.

Properties of Relations:

Reflexiveness e.g. ‘(a). a R a’
Symmetry e.g. ‘(a, b). a R b . ⊃ . b R a’
Transitivity e.g. ‘(a, b, c): a R b . b R c . ⊃ . a R c’

11.

Propositional Calculus.

Uses a Universe of Propositions which are either True (1) or False (O)

p means ‘p is true’ or ‘p=1’, leading to ‘p=(p=1)’.

12.

Calculus of Elementary Propositions.

Used by Principia Mathematica by Russel & Whitehead. Improves on above flawed notation.

† means ‘it is asserted that’ e.g. ‘†: p V q . ⊃ . q V p;

13.

Function and Argument:

A Proposition consists of a Function and Arguments.

e.g. Ï•x instead of p, where f is the function and x is the argument.

We may quantify the argument instead of the whole proposition to show that functions which are not identical are formally equivalent, allowing us to express ‘(x): mortal(x) =
will_die(x)’

Logistics:

Seeks to create a logical foundation for mathematics.

Recommended Reading:

An Introduction to Symbolic Logic: Susanne K. Langer

Godel, Escher, Bach : An Eternal Golden Braid, Douglas R. Hofstadter